大学物理(下)复习
(封面图为我的大物老师田友伟老师,tyw yyds!)
2022.1 更新:这次大物重修终于没有爆炸,成绩 85->98,对量子物理的内容进行修正与补充,并更新其余章节的内容(看了一下贝院大物复习 ppt 从 11年开始已经 11 年没修改过了~)。
标 * 为复习 ppt 中未出现的内容
机械振动
简谐振动:合外力与位移关系为 $F=-kx$ 的振动,运动方程为:
$$
x=A\cos(\omega t+\varphi)\overset{求导}\Longrightarrow v=-\omega A\sin(\omega t+\varphi)\overset{求导}\Longrightarrow a=-\omega^2A\cos(\omega t+\varphi)
$$
其中,$A$ :振幅,反映系统能量大小,与初始条件有关,$A=\sqrt{x_0^2+(\frac{v_0}\omega)^2}(t=0)$$\omega$ :角频率或圆频率,反映振动快慢,系统属性,$\omega=\sqrt{k\over m}=\frac{2\pi}T$
$\varphi$ :初相位,反映谐振子初始时刻振动状态,旋转矢量法中,初始条件绘制的旋转矢量与 $+x$ 轴的夹角即为 $\varphi$
$\omega t+\varphi$:相位或周相或相,反映谐振子振动状态
旋转矢量法:确定初始条件($x_0$、$v_0$ 方向)、画出旋转矢量、确定 $\varphi$
考点1:常见根据坐标图写振动方程,首先看 $x_0$,然后根据 $x_0$ 之后的走向(更负还是更正)判断 $v_0$ 方向,然后就可以画旋转矢量了
考点2:简谐运动的超前与落后,两个简谐运动的相位分别为 $\varphi_1,\varphi_2$,则后一个比前一个超前位相 $\varphi_2-\varphi_1$(如果为负则用 $2\pi$ 补正,一般认为超前位相更少的更超前),超前时间结合 $\omega$ 计算即可,此类题目建议放在旋转矢量图上比较
注意:弹簧类题目注意是否考虑重力!!!
弹簧串联:$k=\frac{k_1k_2}{k_1+k_2}$,弹簧并联:$k=k_1+k_2$,钟摆:$\omega=\sqrt{g\over l}$
简谐振动的动能/势能/总能量
- 振动动能:$E_k=\frac 12 mv^2=\frac 12m\omega^2A^2\sin^2(\omega t+\varphi)=\frac 12kA^2\sin^2(\omega t+\varphi)$
- 振动势能:$E_p=\frac12kx^2=\frac12kA^2\cos^2(\omega t+\varphi)$
- 振动总能量:$E=E_k+E_p=\frac 12 mv^2+\frac12kx^2=\frac12kA^2$
同频率同方向的简谐振动合成
$$
x=x_1+x_2=A\cos(\omega t+\varphi)\
\begin{cases}
A=\sqrt{A_1^2+A_2^2+2A_1A_2\cos(\varphi_2-\varphi_2)}\
\tan \varphi = \frac{ { {A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2} } }{ { {A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2} } }
\end{cases}
$$
波动(波的传播与叠加)
基础概念
横波的振动方向与波的传播方向垂直、纵波的振动方向与波的传播方向平行
产生条件:
- 波源:决定波的频率及其能量
- 弹性媒质:媒质决定波的传播速度(波速)
*平面简谐波:媒质中各质点的运动为简谐振动 任何复杂的波 $(非简谐波)=\sum
(简谐波)$波阵面和波线:波阵面是针对球面波、波线是针对平面波
同一波阵面上各点的运动情况相同(位相相同)
波长 $\lambda$:同一波线上为相差为 $2\pi$ 的两点间的距离
周期 $T$:一个完整波通过某点所需的时间,只与波源有关。频率 $\nu=\frac1T$,角频率 $\omega=\frac{2\pi}T$
波速 $u$:$u=\frac\lambda T=\lambda\nu$,只与媒质有关。一个重要公式:$\frac\omega u=\frac{2\pi\nu}u=\frac{2\pi}\lambda$
波函数(波动方程)
几种标准形式(右行波取
-号,左行波取+号)
$$
y=A\cos[\omega(t\mp \frac x u)+\varphi_0]\
y=A\cos[\frac{2\pi}{T}(t\mp \frac x u)+\varphi_0]\
y=A\cos[2\pi(\frac tT\mp \frac x \lambda)+\varphi_0]\
y=A\cos[\frac{2\pi}\lambda(ut\mp x)+\varphi_0]
$$求解
沿波的传播方向各点相位依次落后: $\varphi_P(t)-\varphi_Q(t)=\omega \Delta t=\omega \frac{\Delta x}u=\frac {2\pi} \lambda \Delta x$
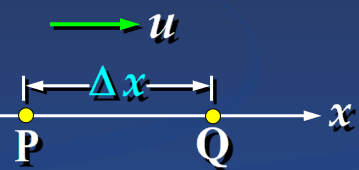
求波函数 $\leftarrow $ 求 $x$ 处质点的振动方程 $\leftarrow$ 求 $\varphi(x,t)=?$ ($\varphi(x,t)-\varphi_Y(x_Y,t)=\omega\frac{x-x_Y}{u}$)
$v(x_0,t_0)=\left.\frac{\partial y}{\partial t}\right|{x_0,t_0},a(x_0,t_0)=\left.\frac{\partial^2 y}{\partial t^2}\right|{x_0,t_0}$
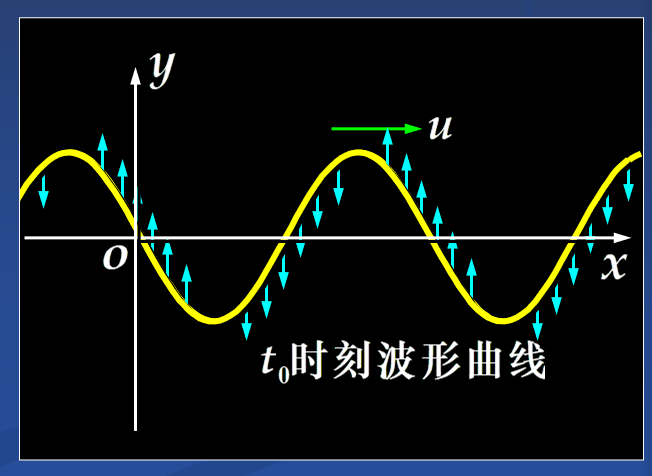
考点:固定 $t$ 后画出波形,判断各点的速度方向或运动趋势 (同侧法:传播方向与振动方向在波的同一侧)
波的能量与能量密度
- $x$ 处的质元质量 $\mathrm{d}m=\rho S \mathrm{d}x$,又由波函数 $y=A\cos[\omega(t-\frac x u)+\varphi_0]$ 得:质元 $dx$ 得动能:
$$
\mathrm{d}E_k = \frac 1 2 (\rho S\mathrm{d}x)(\frac{\partial y}{\partial t})^2=\frac12\rho \mathrm{d}V\cdot \omega^2A^2\cdot \sin^2[\omega(t-\frac x u)+ \varphi_0]
$$任意时刻媒质中某质元的 动能 = 势能 !($\mathrm d E_k = \mathrm d E_p$)
能量密度 $w = \frac{ {\mathrm dE} }{ {\mathrm dV} } = \frac{ {\mathrm dE_k + \mathrm dE_p} }{ {\mathrm dV} }=\rho\omega^2A^2\sin^2[\omega(t-\frac x u) + \varphi_0]=w(t)$
一个周期内能量密度的平均值: $\overline w=\frac 1 T\int_0^T w(t) \mathrm dt = \frac12\rho\omega^2A^2\propto A^2$
波的能流及能流密度
能流:单位时间内垂直通过某界面 $S$ 的能量,$P=\frac{w\cdot Su\mathrm dt}{\mathrm dt}=w\cdot S\cdot u$
平均能流:$\overline P = \overline w\cdot S\cdot u =\frac 1 2 \rho u \cdot \omega^2 A^2\cdot S$
能流密度:$I=\overline P/S=\frac12\rho u\cdot \omega^2A^2\propto A^2$ ,亦称波的强度
惠更斯原理:媒质中波动各点皆可当作球面子波的新波源;任意时刻各子波源所发出子波的包迹即为新波阵面
波的传播具有独立性:相遇后各列波原有特性不变
在相遇空间中的任一点的振动为各列波在该点分别引起的振动位移矢量和:$\vec y(x,t)=\sum_i \vec y_i(x,t)$
波的干涉
相干条件:频率相同;振动方向相同;位相差恒定
满足相干条件的波源/波称为相干波源/相干波
干涉特点:各点 $A$ 不同,但波强 $I$ 稳定分布
两相干波源 $S_1,S_2$ 的振动方程分别为:$y_{S_1}=A_1\cos(\omega t+\varphi_1),y_{S_2}=A_2\cos(\omega t+\varphi_2)$
则可以写出波动方程 $y_k=A_k\cos(\omega(t-\frac x u)+\varphi_k)\overset{\frac \omega u=\frac {2\pi} {T\cdot u}=\frac {2\pi}{\lambda} }{=}A_k \cos(\omega t+\varphi_k-\frac{2\pi}{\lambda}x),k\in{1,2}$
故在 P 点引起的振动为:$y_{1P}=A_1\cos(\omega t+\varphi_1 - \frac {2\pi}{\lambda} r_1),y_{2P} = A_2\cos(\omega t+ \varphi_2 - \frac{2\pi}{\lambda}r_2)$
则相干后:$y_P=y_{1P}+y_{2P}=A\cos(\omega t+\varphi)$,其中 $A=\sqrt{A_1^2+A_2+2A_1A_2 \cos{\Delta\varphi} }$,$\Delta\varphi = (\varphi_2-\varphi_1)-\frac{2\pi}\lambda(r_2-r_1)$($\Delta\varphi$ 就是 $y_{1P},y_{2P}$ 的相位部分做差,$A$ 的式子在机械振动最后出现过类似的)

当 $\Delta\varphi = (\varphi_2-\varphi_1)-\frac{2\pi}\lambda(r_2-r_1)=\pm2k\pi $ 时,干涉加强;当 $\Delta\varphi=\pm(2k+1)\pi$ 时,干涉减弱
原因:当相位相差 $2\pi$ 的整数倍时,旋转矢量方向相同,叠加起来才最大,也就是干涉加强(干涉极大),当相差 $(2k+1)\pi$ 时,旋转矢量恰好方向相反,叠加起来最小,也就是干涉减弱(干涉极小)
波程差:$\Delta r=r_2-r_1 \Rightarrow \Delta\varphi = (\varphi_2-\varphi_1)-\frac{2\pi}\lambda\Delta r$
驻波
形成条件:两列相干波相反方向传播并相遇(是波的干涉的一个特殊情况)
*现象:叠加区域各点振幅不同,但不随时间变化;出现 波节点(振幅为 0)和波腹点(振幅最大)
和差化积公式:$\cos \alpha+\cos \beta = 2\cos({\alpha+\beta\over 2})\cos({\alpha-\beta\over 2})$
驻波方程
两相干波: $y_1=A\cos[2\pi(\frac tT-\frac x\lambda)],y_2=A\cos[2\pi(\frac tT+\frac x\lambda)]$(假设 $\varphi_{1O}=\varphi_{2O}=0$)
合振动:$y=y_1+y_2=[2A\cos(\frac{2\pi}\lambda x)]\cdot cos(\frac {2\pi} T t)=A(x) \cos({2\pi\over T}t)$,其中 $A(x) =2A\cos(\frac{2\pi}\lambda x) $
一些结论:相邻波腹点与波节点距离差为 $x_{k+1}-x_k=\frac \lambda 2$;相邻两个波节点间各点位相相同,运动同向;关于波节点对称的两点位相相差 $\pi$,运动反向!
能量分布(驻波不传播能量)
- 最大位移处:$y=\pm2A$,波节处势能最大
- 平衡位置处:$y=0$,波腹处动能最大
考点:可能会考察给驻波标运动趋势,需要注意的是与行波不同,他是方向均指向 $x$ 坐标轴
半波损失:波由波疏媒质入射到波密媒质在反射时,反射波在反射点与入射波有 $\pi$ 位相突变
入射波与反射波形成的驻波:
波源 $S$ 的振动方程为 $y_o=A\cos(\omega t)$,则 $y_入=A\cos(\omega t-\frac {2\pi}\lambda x)$,$y_{入M}=A\cos(\omega t-{2\pi\over\lambda}x_M)$
而 $M$ 点位移大小 $y_M=y_{入M}+y_{反M}=0$,故 $y_{反M}=A\cos(\omega t-\frac{2\pi}\lambda x_M + \pi)$
此时 $M$ 可看为反射源,故 $y_反=A\cos[\omega t-{2\pi\over \lambda}x_M+\pi - {2\pi\over \lambda}(x_M-x)]$$=A\cos(\omega t+{2\pi\over \lambda}x-{4\pi\over \lambda}x_M + \pi)$(反射波波函数)
此时驻波: $y=y_入+y_反=A(x)\cos(\omega t-{2\pi\over\lambda}x_M+\frac \pi 2),A(x) = 2A\cos[{2\pi\over \lambda}(x-x_M)+\frac \pi 2]$

注:自由端反射无半波损失(自由端为波腹点,比如摇绳子)
两端固定的线上,形成稳定的驻波条件:$l=n\cdot {\lambda\over 2}\Rightarrow \lambda_n=\frac{2l}n$,频率需满足:$\nu_n=\frac u \lambda = n {u\over 2l}$

普勒效应
观测频率 $\nu = \frac{u+v_B}{u-v_S}\nu_0$($S$ 为波源,$B$ 为观测者,两者速度方向相对时 $v_S,v_B$ 均为正数),计算反射频率时,先认为反射壁为观测者,计算出的频率即为反射频率,拍频为观测频率与观测反射频率(就是认为反射壁为波源)做差
电磁波
*单色平面电磁波波函数:
$$
\begin{cases}
E=E_0\cos(\omega t- kx)\
H=H_0\cos(\omega t - kx)
\end{cases}
$$
波矢:$\lvert \vec k\rvert=\frac{2\pi}\lambda$电磁波的主要特性:横波特性:$\vec E \perp \vec H \perp \vec k$;$\vec E$ 和 $\vec H$ 同位相;$\vec E$ 和 $\vec H$ 的数值成比例:$\frac E H=\sqrt\frac {\mu}{\varepsilon}$ 或 $\sqrt \varepsilon = \sqrt \mu H$;真空中电磁波波速=真空中光速:$u=\frac 1 {\mu_0\varepsilon_0}\approx 2.998\times 10^8 m/s=c$
电磁波的能流密度 $\vec S = \vec E\times \vec H$(称为波印亭矢量),平均波印亭矢量:$\overline S=\frac12E_0H_0$
光学(光的干涉、衍射与偏振)
相干光
获得相干光的两种方法:分波阵面法、分振幅法
光波在传播空间的光程 $L$ 满足:$光程L=媒质折射率 n\times 几何路程 r$
物理意义:$L=nr=\frac c v r=c\frac r v=c\Delta t$,即 $L$ 可折算成在相等的时间内,光在真空中所走过的路程
光程差 $\delta$ 与相位差 $\Delta\varphi$ 的关系:$\Delta \varphi = {2\pi\over\lambda_2 }r_2 - {2\pi\over \lambda_1}r_1={2\pi\over \lambda_0}(n_2r_2-n_1r_1)$,令 $\delta=n_2r_2-n_1r_1$ 即光程差,则 $\Delta \phi = {2\pi\over \lambda_0}\delta$
注:
- 透镜不引起额外光程差
- 当光从光疏媒质到光密媒质反射时,入射光与反射光间亦有半波损失现象:$\delta=L_2-L_1+{\lambda \over 2}$$=(由几何路径差引起)+(额外光程差)^*$
杨氏双缝干涉
由 $\Delta \varphi = \begin{cases}\pm 2k\pi&干涉加强\rightarrow 明纹\\pm(2k+1)\pi&干涉减弱\rightarrow 暗纹\end{cases}$,$\Delta \varphi={2\pi \over \lambda}\delta$,得:
$$
\delta = \begin{cases}\pm 2k\frac\lambda 2&干涉加强\rightarrow 明纹\\pm(2k+1)\frac\lambda 2&干涉减弱\rightarrow 暗纹\end{cases}
$$干涉条纹位置分布
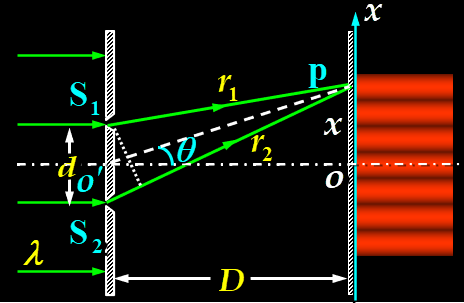
设入射光垂直入射,$d\ll D,x\ll D$
则 $\delta= r_2-r_1\approx d\cdot \sin\theta$($\theta$ 称为衍射角),而 $\sin\theta = \tan \theta = \frac x D$,则 $\delta= r_2 - r_1 \approx d\cdot \frac x D= \begin{cases}\pm 2k\frac \lambda 2& 明纹\ \pm(2k+1)\frac\lambda 2& 暗纹\end{cases}$
则明纹位置:$x_k=\pm \frac D d\cdot 2k\cdot \frac \lambda 2(k=0,1,2,\cdots)$
中央明纹:$k=0,\delta= 0$,其他所有明纹关于中央明纹对称
相邻两条明(暗)纹间距:$\Delta x = \lvert x_{k+1}-x_k\rvert = \frac D d\lambda$
干涉图样:平行等间距的直条纹
斜入射:$\delta= \delta_1 + \delta_2 = d\cdot \sin \theta + d\cdot \sin \alpha = d\cdot (\sin \theta + \sin \alpha)= \begin{cases}\pm 2k\cdot \frac \lambda 2& 明纹\ \pm(2k+1)\cdot \frac\lambda 2& 暗纹\end{cases}$,中央明纹出现在:$\delta= d\cdot(\sin \theta+\sin\alpha) = 0\rightarrow \theta = -\alpha$

白光入射:相邻条纹间距 $\Delta x = \frac D d\lambda \propto\lambda$
分波阵面法干涉
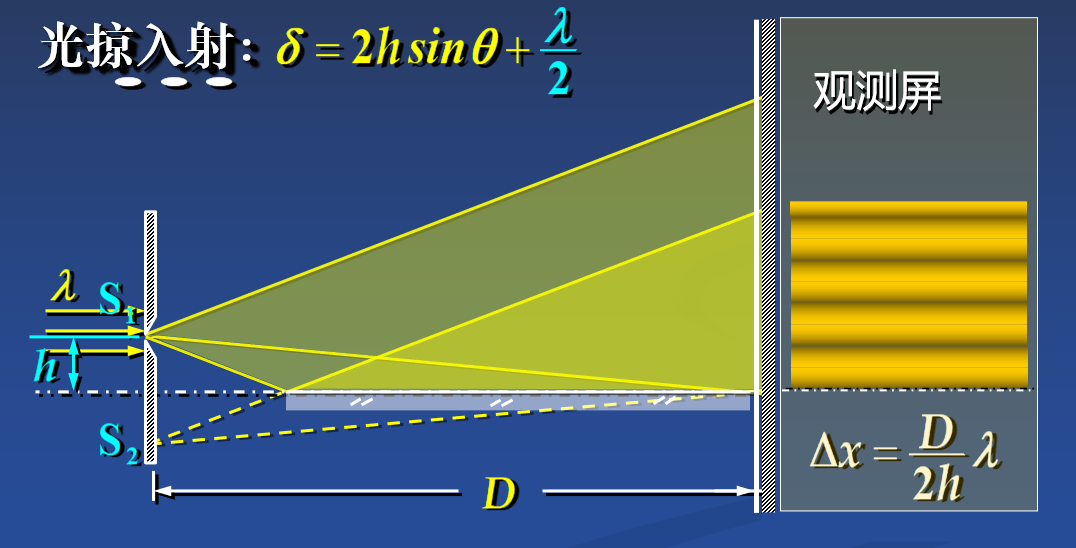
薄膜干涉(只有反射且波疏到波密有半波损失,折射没有半波损失)
由 $\delta= (n_2 \cdot \overline{
ACB} - n_1\cdot \overline {AD})+\left[{\lambda\over 2}\right]^*$ (是否有 $\lambda\over 2$ 要看 $n_1,n_2,n_3$ 的关系)而 $\overline {ACB} = {2e\over \cos\gamma} , \overline{AD} = 2e\cdot \tan\gamma\cdot \sin i$
又因为折射定律:$n_1\cdot \sin i = n_2 \cdot \sin \gamma$可得:$\delta= 2e\sqrt{n_2^2-n_1^2\cdot \sin^2i}+\left[{\lambda \over 2}\right]^*= \begin{cases} 2k\frac \lambda 2& 明纹\ (2k-1)\frac\lambda 2& 暗纹\end{cases}$(此处 $\delta\ge 0, k\ge 0$)

对于 $\delta= \delta(e,i,\lambda)$
当 $e,i$ 一定时,$\delta= \delta(\lambda)$,为选择性干涉
增透膜:使反射光干涉相消 $\delta_反=2n_2e=(2k-1){\lambda\over 2}$
增反膜:使反射光干涉相长 $\delta_反=2n_2e+{\lambda\over 2}=2k{\lambda\over 2}$
当 $i,\lambda$ 一定时,$\delta= \delta(e)$,为等厚干涉
$e$ 相同的点在同一级干涉级次上,即干涉场中的等厚线形状即为干涉图样
当 $\lambda,e$ 一定时,$\delta= \delta(i)$,为等倾干涉
劈尖(真空 $n=1$,空气 $n\approx 1$,其他透光物质 (水、玻璃、云母片等) $n>1$)
设光垂直入射,故 $i\approx0$
则空气劈尖中有:$\delta= 2e\sqrt{n_2^2-n_1^2\cdot \sin^2i}+{\lambda\over 2} = 2e+{\lambda\over 2}=\begin{cases}2k{\lambda\over 2}&明\(2k-1){\lambda\over 2}&暗\end{cases}(k=1,2,\cdots)$当 $e=0$ 时,$\delta = {\lambda\over 2}$,故空气劈尖的底边为暗纹
此外,第 $k$ 级条纹厚度 $e_k=\begin{cases}(k-\frac12){\lambda\over 2}&明纹\(k-1){\lambda\over 2}&暗纹\end{cases}(k=1,2,\cdots)$
相邻两明纹(或暗纹)的厚度差 $\Delta e = {\lambda\over 2}$,对于 $n\neq1$ 的劈尖:$\Delta e = {\lambda\over 2n}$
又因 $\Delta e =l\cdot \sin\alpha \approx l\cdot \alpha $,故条纹面间距:$l={\lambda\over 2n\alpha}$
利用劈尖干涉测量小物体尺寸:干涉明 (暗) 纹总数为 $N$,则小物体高度为 $h\approx (N-1)\cdot \Delta e$,其中 $\Delta e= {\lambda\over 2n}$
利用劈尖干涉可以测量工件的平整程度,不平整的工件条纹不是直线
牛顿环
明、暗环半径:$r_k=\begin{cases}\sqrt{(2k-1)R\lambda/2}&明环\\sqrt{(k-1)R\lambda }& 暗环\end{cases}$
相邻两暗环半径差:$r_{k+1} -r_k=\sqrt{R\lambda}(\sqrt k - \sqrt{k-1})$
条纹特点:越往外条纹越密集,且级次 $k$ 增加
利用牛顿环测量透镜曲率半径:$R=\frac{r_{k+m}^2-r_k^2}{m\lambda}$
等倾干涉
迈克尔逊干涉仪:$\Delta d = N{\lambda\over2}$($N$ 为从中心冒出的条纹数,$\Delta d$ 为光路的变化长度,不用$\times2$ !!!)
样品厚度:$d = \frac{N} {n-1}\frac \lambda2$($n$ 为样品的折射率,这个公式也就是令上面公式里的 $\Delta d=n\cdot d-d$,即光路里面插入了一片样品)
惠更斯—菲涅尔原理
惠更斯原理 + 从同一波阵面 $S$ 上各点所发出的子波,传播至某点相遇时,也可相干叠加,产生干涉现象。
衍射
- 干涉与衍射的区别:干涉是有限个波的叠加,如双光波、多光波;衍射是无限个波的叠加
- 衍射的分类:近场衍射(当光源或观察屏到衍射物的距离为有限远时)、远场衍射(当光源或观察屏到衍射物的距离为无限远时)
单缝衍射
- $a\cdot \sin\theta = \begin{cases}\pm 2k{\lambda\over 2}& 暗纹\ \pm(2k+1){\lambda\over 2}& 明纹\end{cases}(k=1,2,\cdots)$,$a$ 为单缝的宽度,$\theta$ 为半角宽度且 $\sin\theta = \tan\theta = \theta$
- 衍射反比律 中央明纹半角宽度 $\theta_1 \approx{\lambda\over a}$,角宽度 $2\theta_1={2\lambda\over a}$
- 中央明纹宽度 $2x_1=2f\cdot \tan\theta_1\approx 2f\cdot \theta_1={2f\lambda\over a}$
- 其他明纹宽度 $\Delta x= x_2-x_1\approx {f\lambda\over a} = $ 中央明纹宽度的一半
- 中央明纹最宽(为其他明纹宽度的两倍)最亮(绝大部分能量集中在中央明纹区域内)
- 缝平面上下平移,条纹的位置不变;只有透镜上下移动条纹才会随之上下移动
- 白光入射(并不知道考啥)
圆孔衍射
- 光学仪器的最小分辨角 $\delta\theta = {1.22 \lambda\over D}$(可分辨:$\theta\ge\delta\theta$,$\lambda$ 为波长,$D$ 为孔径)
- 可分辨的高度:$h\approx l\cdot \theta\ge l\cdot \delta\theta$,可分辨的距离:$l\approx \frac h \theta \le \frac h {\delta\theta}$
- 光学仪器的分辨本领:$R=\frac 1 {\delta\theta}= \frac D{1.22\lambda}$
- 提高分辨本领的两个途径:使 $D\uparrow$(增加孔径,如天文望远镜)或 $\lambda\downarrow$(减小波长,如电子显微镜)
衍射光栅
光栅常数 $d=a+b$($a$ 为缝宽,$b$ 为片宽度,$N$ 为总缝数)
不考虑缝宽 $b\gg a$:
- 明纹条件(光栅方程):$\delta= d\cdot \sin \theta=\pm k\lambda (k=0,1,2,\cdots)$ ,该方向明纹称为明纹主极大
- 暗纹条件:相邻两个主极大间共有 $N-1$ 条暗纹,相邻两明纹主极大间共有 $N-2$ 个次极大,光强较小
- 条纹特点:$N$ 较大时,背景较暗,明纹细窄、明亮
考虑缝宽 $a$:($k’=1,2,\cdots;k=0,1,2,\cdots$)
暗纹条件:$a\cdot \sin\theta=\pm2k’\cdot \frac \lambda 2$ 或 $d\cdot \sin\theta=\pm(2k+1)\cdot \frac \lambda 2$
明纹条件:$d\cdot \sin\theta=\pm k\lambda$ 且 $a\cdot \sin\theta\neq\pm2k’\cdot \frac \lambda 2$
缺级现象:若 $\theta$ 满足 $d\cdot \sin\theta=\pm k\lambda$ 且 $a\cdot \sin\theta = \pm2k’\cdot \frac \lambda 2$,$k$ 级主极大消失,称为缺级现象
所缺的主极大级次:$k=\pm \frac da k’=\pm \frac da,\pm \frac {2d}a.\pm \frac{3d}a,\cdots$
中央明带内的条纹数:$2\times(\frac d a-1)+1$
光的偏振,马吕斯定律
- 振动面:电矢量 $\vec E$ 与传播方向构成的面
- 线偏振光(平面/完全偏振光):点表示垂直于屏幕,竖线表示平行于屏幕
- 自然光:光矢量 $\vec E$ 沿任意方向概率相同,属于非偏振光,用点和竖线的叠加表示,$I_x = I_y = \frac12 I_0$
- 部分偏振光:光矢量 $\vec E$ 沿某一方向占优势
- 马吕斯定律:光强 $I_2 = I_1\cdot \cos^2\alpha$
- 应用:$自然光\overset{偏振片}\longrightarrow 偏振光: I_1=\frac {I_0} 2$,$偏振光\overset{偏振片}\longrightarrow 偏振光:I_2=
I_1\cdot \cos^2 \alpha$
布儒斯特定律:当入射角 $i=i_0$ 时,反射光为线偏振光,而 $\tan i_0=\frac{n_2}{n_1}$,其中 $i_0$ 为布儒斯特角/起偏振角,且反射光线 $\perp$ 折射光线
一束光遵从折射定律:称为寻常光,或 o 光
另一束不遵从折射定律:称为非寻常光,或 e 光
o 光和 e 光皆为线偏振光,且振动方向相互垂直。
狭义相对论和量子物理
洛仑兹坐标和速度变换★★★
$S$ 为固定参考系,$S’$以速度 $v$ (相对速度)沿 $x$ 轴正方向运动(坐标系重合时 $t=t’=0$)。
定义:$\beta = {v\over c}$,膨胀因子 $\gamma = {1\over \sqrt{1-\beta^2} }\ge 1$
坐标变换:
$$
\begin{aligned}
S\rightarrow S’
\begin{cases}
x’=\gamma(x-vt)\
y’=y;z’=z\
t’=\gamma(t-\beta{x\over c})
\end{cases}
&&
S’\rightarrow S
\begin{cases}
x=\gamma(x’+vt’)\
y=y’;z=z’\
t=\gamma(t’+\beta{x’\over c})
\end{cases}
\end{aligned}
$$
速度变换:
$$
\begin{aligned}
\begin{cases}
u_x’=\frac{u_x-v}{1-\beta{u_x\over c} }\
u_y’=\frac{u_y}{\gamma(1-\beta{u_x\over c})}\
u_z’=\frac{u_z}{\gamma(1-\beta{u_x\over c})}
\end{cases}
&&
\begin{cases}
u_x=\frac{u_x’-v}{1+\beta{u_x’\over c} }\
u_y=\frac{u_y’}{\gamma(1+\beta{u_x’\over c})}\
u_z=\frac{u_z’}{\gamma(1+\beta{u_x’\over c})}
\end{cases}
\end{aligned}
$$狭义相对论时空观★★
时间间隔与空间间隔:($\Delta x,\Delta t$:静止参考系;$\Delta x’,\Delta y’$:相对以速度 $v$ 运动参考系)
$$
\begin{aligned}
\begin{cases}
\Delta x’=\gamma(\Delta x-v\Delta t)\
\Delta t’=\gamma(\Delta t-{v\Delta x\over c^2})
\end{cases}
&&
\begin{cases}
\Delta x=\gamma(\Delta x’-v\Delta t’)\
\Delta t=\gamma(\Delta t’+{v\Delta x’\over c^2})
\end{cases}
\end{aligned}
$$
时间膨胀:$\Delta t=\gamma \tau \ge \tau$( $\tau$ 为固有时间)长度收缩:$l=l_0\sqrt{1-{v^2\over c^2} }$( $l_0$ 为固有长度)
因果关系: 有因果关系的两事件发生的时序不会颠倒,因果律对任何惯性参照系都是不变的。
(同地同时与参考系无关,是绝对的;异地同时与参考系有关,是相对的)狭义相对论质量、动量、能量、动能★★★
$m_0$:物体静止质量,$m$:物体运动时的质量
质量:$m={m_0\over\sqrt{1-({v_m\over c})^2} }$
动量:$\vec P=m\vec v_m = {m_0\vec v_m\over\sqrt{1-({v_m\over c})^2} } $
能量:物体以速度 $v$ 运动时的总能量:$E=mc^2={m_0\vec c^2\over\sqrt{1-({v_m\over c})^2} }$ (质量亏损的质能方程:$\Delta E=\Delta mc^2$)
动能:$E_k=mc^2-m_0c^2$
动量与能量间的关系: $E^2=E_0^2+P^2c^2$
黑体辐射★
辐出度 $M(T)=\int_0^\infty M_\lambda(T)\mathrm d\lambda=\sigma T^4$
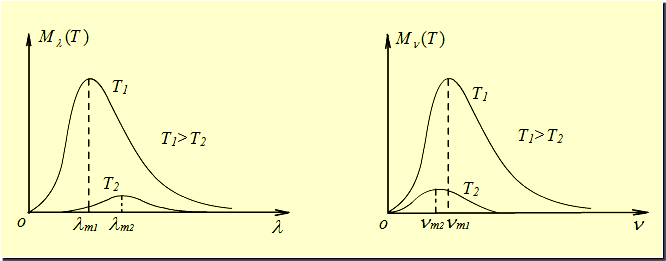
维恩位移定律 $\lambda_m T=b$
当黑体的热力学温度升高时,$M_\lambda(T)\sim\lambda$ 曲线上单色辐出度所对应的峰值波长 $\lambda_m$ 向短波方向移动,且 $\lambda_mT=b$
光电效应、康普顿效应★★★
爱因斯坦方程:$h\nu = \frac{1}{2}mv^2+W$($W$ 为逸出功)
$v$ 为光电子的速度,要使光电子逃逸出金属表面,必须使 $E_k=h\nu-W\ge0$,即$v\ge {W\over h}$
截止频率(红限频率)$v_0={W\over h}$
反向遏止电压(电势差) $U_0$ 满足 $eU_0=h\nu-W$
$I = N \cdot h\nu $
$E=h\nu,p={h\over \lambda}$
康普顿效应:$x$ 射线通过物质时散射线中除了有与入射波长 $\lambda_0$ 相同的射线外,还有 $\lambda>\lambda_0$ 的射线
康普顿效应证明了光量子理论
碰撞过程中,光子和电子组成的系统能量和动量守恒:
$\begin{cases}h\nu_0+m_0c^2=h\nu+mc^2&(1)\\ {h\nu_0\over c}\vec e_0={h\nu\over c}\vec e+m\vec v&(2)\end{cases}$光子能量:${hc\over \lambda}={hc\over \lambda_0}-E_k$
电子获得能量:$\Delta E= E_k=mc^2-m_0c^2,其中,m={m_0\over \sqrt{1-({v\over c})^2} }$
$\Delta\lambda=\lambda-\lambda_0={h\over m_0c}(1-\cos\theta)$
$\Delta \lambda = 2\lambda_c\sin^2{\theta\over 2}={2h\over m_0c}\sin^2{\theta\over 2}$($\lambda_c={h\over m_0c}$ 称作康普顿波长)
德布罗意波、光和实物粒子的波粒二象性★★
实物粒子具有波粒二象性
德布罗意关系:$E=mc^2=h\nu,p=mv={h\over \lambda}$,德布罗意公式:$\lambda = {h\over p}={h\over mv},\nu = {E\over h}={mc^2\over h}$
德布罗意波是概率波:强度是与粒子在该处邻近出现的概率成正比的
不确定关系★
$\Delta x$:$x$ 方向位置不确定量, $\Delta p_x$:$x$ 方向动量不确定量
$$
\begin{cases}
\Delta x\cdot \Delta p_x \ge h\
\Delta y\cdot \Delta p_y \ge h\
\Delta z\cdot \Delta p_z \ge h
\end{cases}
$$定态薛定谔方程、无限深势阱问题★★★
- 自由粒子平面波函数:$\psi(x,t)=\psi_0 e^{-i{2\pi\over h}(Et-px)}$
- 波函数的统计意义:概率密度 $\lvert \Psi\rvert^2=\psi\psi^*$
- 归一化条件:$\int \lvert\Psi\rvert^2 \mathrm dV=1$
- 在势场中一维运动粒子的定态薛定谔方程:${\mathrm d^2\psi\over \mathrm dx^2}+{8\pi^2m\over h^2}(E-E_p)\psi(x) = 0$
- 一维无限深势阱问题
- 波动方程:
- 波函数 $\psi(x)=\sqrt{2\over a}\sin {n\pi\over a}x$
- 概率密度 $w_n(x)=|\psi_n(x)|^2=\frac2a\sin^2\frac{n\pi}ax$
- 能量 $E=n^2{h^2\over 8ma^2}$,
氢原子、激光、半导体基础知识(自学内容)★
四个量子数与角动量
原子中的电子的运动状态可由四个量子数($n, l ,m_l , m_s$) 来表示
量子化的能量 $E_n=\frac 1 {n^2}E_1$ $n=1,2,3,\cdots$ 为主量子数
$E_1=-{me^4\over 8\varepsilon_0^2h^2}=-13.6(eV)$
角动量 $L=\sqrt{l(l+1)}\frac h {2\pi}$,$l=0,1,2,3,\cdots,(n-1)$ 为角量子数
角动量量子化的空间取向 $L_z=m_l{h \over 2\pi}$,$m_l=0,\pm1,\pm2,\cdots,\pm l$ 为磁量子数
自旋角动量 $S=\sqrt{s(s+1)}{h\over 2\pi} $,式中自旋量子数 $s=\frac 12$,即 $S=\frac{\sqrt3} 2{h\over 2\pi}$
$S_z=m_s{h\over 2\pi}$
$m_s=\pm\frac12$,$m_s$ 称为自旋磁量子数
泡利不相容原理:量子数为 $n$ 时,电子的量子态数(或第 $n$ 壳层最多能容纳的电子数)为 $z_n=\sum_{l=0}^{n-1}2(2l+1)=2n^2$